Y - y 1 -1m x - x 1 B 10 -2 and m 15 y - -2 -1 15 x - 10. October 27th 2020No Comments Uncategorised.
Similar Right Triangles Fully Explained W 9 Examples
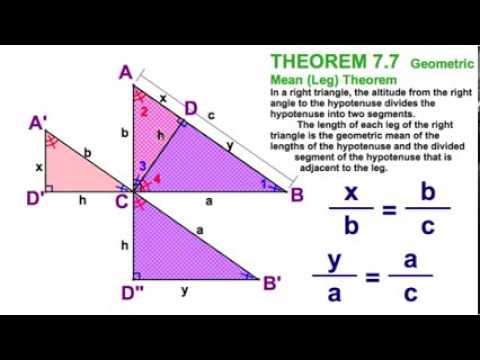
When we construct an altitude of a triangle from a vertex to the hypotenuse of a right-angled triangle it forms two similar triangles.
Formula for altitude of a right triangle. Altitude of side c h NOT CALCULATED. A triangle in which one of the angles is 90 is called a right triangle or a right-angled triangle. No angles are equal.
To calculate the altitude of a triangle you need to find the area of the triangle. The altitude A E is perpendicular to side B C. The slope of side B C is.
That can be calculated using the mentioned formula if the lengths of the other two sides are known. The formula for the one from the apex is. The third altitude of a triangle may be calculated from the formula That can be calculated using the mentioned formula.
This line containing the opposite side is called the extended base of the altitude. Altitude of a Triangle. Select to solve for a different unknown.
Altitude of a right triangle formula. The pythagorus formula states that the hypotenuse squared is equal to the altitude squared plus the base squared. Since the altitude A E passes through the point A 3 2 using the point-slope form of the equation.
The intersection of the extended base and the altitude is called the foot of the altitude. Constructing an altitude from any base divides the equilateral triangle into two right triangles each one of which has a hypotenuse equal to the original equilateral triangles side and a leg that length. It states that in a right-angled triangle the square of the hypotenuse is equal to the sum of the squares of the other two sides ie c 2 a 2 b 2.
Now using the area of a triangle and its height the base can be easily calculated as Base 2 AreaHeight Altitudes of Different Triangles. The relation between the sides and angles of a right triangle is the basis for trigonometry. The formula is derived from Pythagorean theorem The heights from base vertices may be calculated from eg.
This formula is true for all right triangles regardless of the lengths of their sides. These equations apply to any type of triangle. This is the required equation of the altitude from C to A B.
There are two different heights of an isosceles triangle. Southern Cross Showjumpers altitude of a right triangle formula. Area of a triangle is base height.
8 4 3 5 12 2 6. In geometry an altitude of a triangle is a line segment through a vertex and perpendicular to ie forming a right angle with a line containing the base the side opposite the vertex. The main use of the altitude is that it is used for area calculation of the triangle ie.
A E 1 slope of B C 1 6. Solving for altitude of side c. Length of side a unitless.
AB BC AC Const. The other leg of the right triangle is the altitude of the equilateral triangle. If you let h the hypotenuse and b equal the base and a equal the altitude then the formula.
Geometry calculator for solving the altitude of side c of a. In the above right triangle BC is the altitude height. The three altitudes of a triangle intersect at the orthocenter H which for a right triangle is in the vertex C of the right angle.
In a right triangle the altitude of each leg a and b is the corresponding opposite leg. Altitude of a Right Triangle. Thus h a b and h b a.
The altitude of the hypotenuse is h c. It is popularly known as the Right triangle altitude. The different parts of a right triangle are as follows.
After you have do. If 3 sides are given you can use herons formula and if 2 sides and the included angle is given you can use the sine area rule to find the area. Let AB be 5 cm and.
That can be calculated using the mentioned formula if the lengths of the other two sides are known. This line containing the opposite side is called the extended base of the altitude. No sides have equal length.
H a - 05 b where a is a leg of the triangle and b a base. The right triangle is composed of the altitude and the base and the hypotenuse. Equation of the altitude passing through the vertex B.
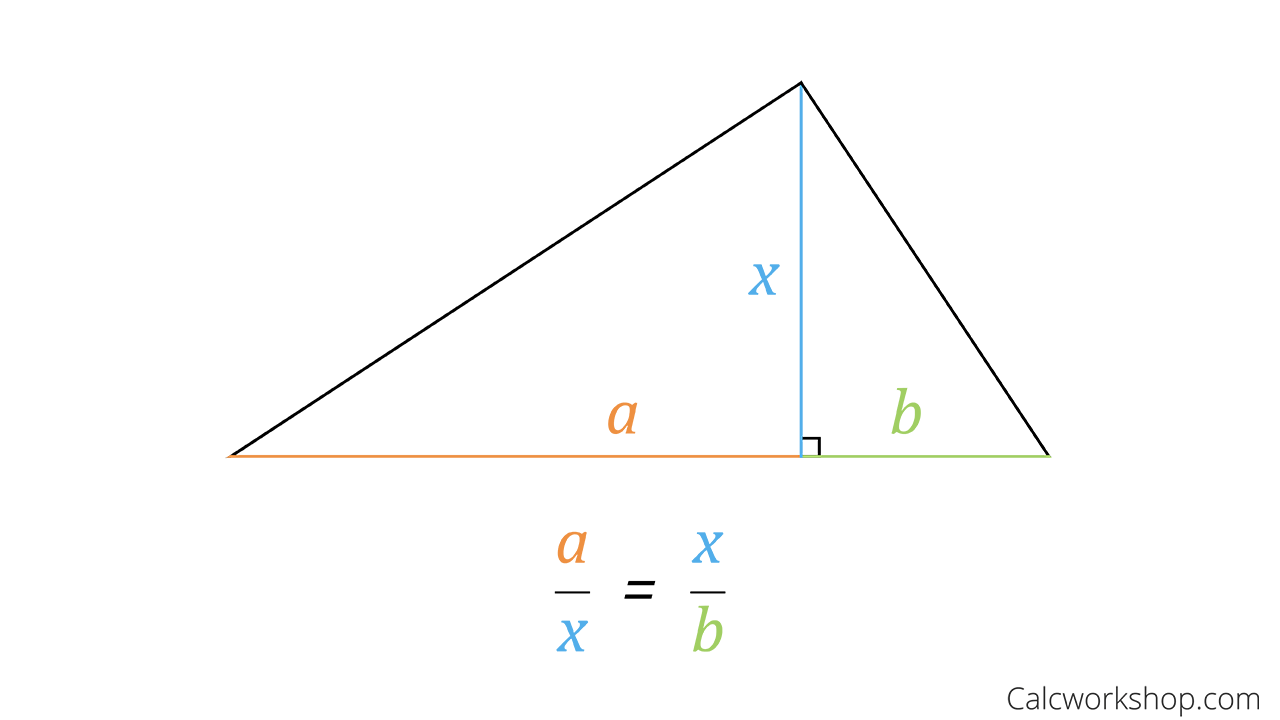
Similar Right Triangles Fully Explained W 9 Examples
Pythagorean Theorem And Right Triangle Formulas Plane Geometry College Elearning
Altitude Of A Triangle Mathematical Way
Altitude Of A Triangle Definition Formulas And Examples
Altitude On Hypotenuse Theorem Plantrigonometry
Using Similar Right Triangles Ck 12 Foundation
Question Video Finding The Length Of The Altitude In A Right Angled Triangle Given The Triangle S Dimensions Nagwa
How To Solve Problems With The Altitude 0n Hypotenuse Theorem Dummies
Determine The Altitude Of A Right Triangle Given Its Side Lengths Youtube
How To Find The Altitude Of A Right Triangle Youtube
Altitude Of A Triangle Definition Formulas Properties Examples
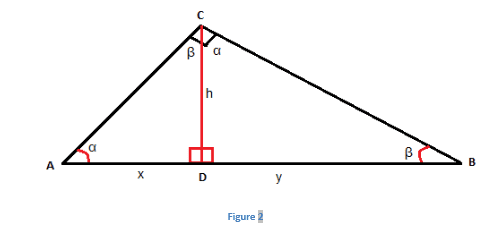
Altitude Of A Triangle Definition Formulas And Examples
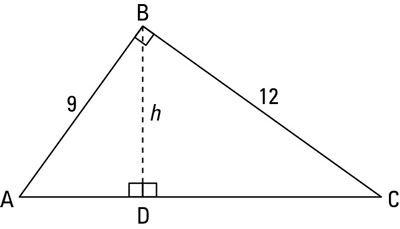
Ex 4 2 5 The Altitude Of A Right Triangle Is 7 Cm Less
Using Similar Right Triangles Ck 12 Foundation
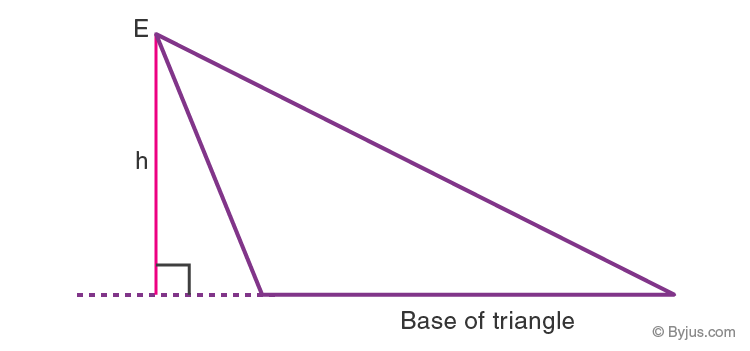
Altitude Of A Triangle Definition Formulas And Examples
Finding The Altitude To The Hypotenuse Of A Right Triangle Youtube
How To Find The Altitude Of A Right Triangle Youtube
7 3 Altitude To Hypotenuse Three Theorems Youtube
How To Measure The Altitude Of A Right Triangle Quora
